안녕하세요.
오늘은 C++로 2D 충돌 처리를 구현해봅시다.
Part 1에서는 AABB, 원, 볼록 다각형을 구현해보고
Part 2에서는 요걸 응용해서 RoundRect나 오목 다각형도 만들어 볼겁니다.
Reference
- https://gamedevelopment.tutsplus.com/series/how-to-create-a-custom-physics-engine--gamedev-12715
How to Create a Custom Physics Engine - Envato Tuts+ Game Development Tutorials
There are many reasons you might want to create a custom physics engine: first, learning and honing your skills in mathematics, physics and programming are great reasons to attempt such a project;...
gamedevelopment.tutsplus.com
- https://github.com/RandyGaul/ImpulseEngine
GitHub - RandyGaul/ImpulseEngine: Simple, open source, 2D impulse based physics engine for educational use.
Simple, open source, 2D impulse based physics engine for educational use. - GitHub - RandyGaul/ImpulseEngine: Simple, open source, 2D impulse based physics engine for educational use.
github.com
Result
Reference를 참고해 만든 라이브러리 입니다.
https://github.com/Kareus/SP2C
GitHub - Kareus/SP2C: A simple 2d collision detection library written in C++
A simple 2d collision detection library written in C++ - Kareus/SP2C
github.com
1. AABB

AABB (Axis Aligned Bounding Box)는 축 방향과 변이 평행한 사각형을 의미합니다.
그렇기 때문에 각도(orientation)가 존재하지 않으며, 충돌 감지가 가장 간단한 편입니다.
이와 대조하여 각도가 존재하는 Bounding Box는 OBB(Oriented Bounding Box)라고 합니다.
여기서 OBB는 다루지 않겠습니다. 사실, 아래에서 다룰 Polygon에 포함되기 때문이기도 합니다.

앞서 말했듯이 AABB 간의 충돌 감지는 간단합니다.
AABB의 좌상단 꼭짓점을 min, 우하단 꼭짓점을 max라고 했을 때
한쪽 사각형의 max.x < min.x 또는 min.x > max.x를 만족한다면
x축에서 두 사각형은 만나지 않는다는 것을 알 수 있습니다.
이는 y축에 대해서도 마찬가지이며, 두 사례에 해당되지 않으면, 두 사각형은 반드시 만나게 됩니다.
코드로 나타내면 다음과 같습니다.
struct Vec2
{
double x;
double y;
};
struct AABB
{
Vec2 min;
Vec2 max;
};
bool AABB_to_AABB(AABB a, AABB b)
{
if (a.max.x < b.min.x || a.min.x > b.max.x) return false;
if (a.max.y < b.min.y || a.min.y > b.max.y) return false;
return true;
}
1-1. Manifold
충돌 처리를 하다보면 충돌이 어느 지점에서 발생했는지, 충돌의 크기는 어느 정도인지, 충돌 방향은 어디인지 알아야 하는 경우가 있습니다. 특히 게임을 개발할 때는 이 정보가 유용합니다.
이를 계산하기 위해서는 단순한 충돌 감지 외에 필요한 작업이 더 있으며, 여기서는 이를 계산해서 Manifold라는 구조체에 담아줄 겁니다.
struct Manifold
{
unsigned int contact_count; //contact point count
Vec2 contact_points[2]; //contact points
Vec2 normal; //contact normal
double penetration; //contact penetration
};여기서 normal은 단위 벡터로 가정하겠습니다.
먼저 AABB에서 충돌 정보를 구하기 위해서는, 충돌의 방향이 x축인지 y축인지부터 알 필요가 있습니다.
이건 각 방향으로 얼마나 겹쳤는지 구하면 간단하게 알 수 있습니다.

AABB의 중심 center = (min + max) / 2, 길이의 절반 extent = (max - min) / 2 라고 합시다.
두 AABB가 겹칠 때, 중심 좌표의 차는 extent의 합 이하임을 알 수 있습니다.
또한 겹친 정도를 (extent의 합) - (중심 좌표의 차)로 구할 수 있습니다.
이를 x_overlap, y_overlap이라고 하고, 둘 중 크기가 더 작은 (얕은) 방향을 골라서 계산하도록 합시다.
두 값은 0 이상의 값임이 보장되기 때문에, 절댓값 처리할 필요가 없습니다.
*** reference로 올린 튜토리얼 페이지에서는 부호가 반대로 되어 있는데, 잘못된 것 같네요.

x축의 경우, 충돌 방향은 (-1, 0) 혹은 (1, 0)입니다. 여기서는 두 도형을 A와 B라고 할 때
A -> B 방향을 선택하도록 하겠습니다. 위에서 구한 중심 좌표의 차가 양수인지 음수인지에 따라 선택하면 됩니다.
충돌의 크기는 겹친 정도 (여기서는 x_overlap)가 됩니다.
충돌한 지점은... 충돌한 상대 도형 (B)에 가장 가까운 A의 지점으로 구했습니다.
일단은 그런 것 같습니다. reference에는 이거에 대한 설명이 없네요.
AABB의 특성상 조건을 만족하는 점이 여러 개이기 때문에, 가능한 끝점 두개를 계산했습니다.
위의 충돌 감지 함수와는 코드의 흐름이 다릅니다.
bool AABB_to_AABB(AABB a, AABB b, Manifold* m)
{
m->contact_count = 0;
Vec2 centerA = (a.min + a.max) / 2;
Vec2 centerB = (b.min + b.max) / 2;
Vec2 n = centerB - centerA;
Vec2 extentA = (a.max - a.min) / 2;
Vec2 extentB = (b.max - b.min) / 2;
double x_overlap = extentA.x + extentB.x - abs(n.x);
double y_overlap = extentA.y + extentB.y - abs(n.y);
if (x_overlap < 0 || y_overlap < 0) return false;
if (x_overlap < y_overlap)
{
if (n.x < 0) m->normal = Vec2(-1, 0);
else m->normal = Vec2(1, 0);
m->penetration = x_overlap;
m->contact_count = 2;
m->contact_points[0] = Vec2((n.x < 0 ? a.min.x : a.max.x), max(a.min.y, b.min.y));
m->contact_points[1] = Vec2(m->contact_points[0].x, min(a.max.y, b.max.y));
}
else
{
if (n.y < 0) m->normal = Vec2(0, -1);
else m->normal = Vec2(0, 1);
m->penetration = y_overlap;
m->contact_count = 2;
m->contact_points[0] = Vec2(max(a.min.x, b.min.x), (n.y < 0 ? a.min.y : a.max.y));
m->contact_points[1] = Vec2(min(a.max.x, b.max.x), m->contact_points[0].y);
}
return true;
}
1-2. Generalization in Manifold
다른 도형에 대한 충돌을 계산할 때도 Manifold를 쓸 수 있도록 해봅시다.
먼저 도형에 대한 기본적인 Base Class를 만들겠습니다.
struct Shape
{
//...
};
struct AABB : public Shape
{
//...
};Manifold에는 어느 두 도형의 충돌을 계산하는지 가리킬 포인터가 두 개 필요합니다.
struct Manifold
{
Shape* A;
Shape* B;
//...
};
함수는 다음과 같이 수정하면 됩니다.
bool AABB_to_AABB(Manifold* m)
{
AABB* a = reinterpret_cast<AABB*>(m->A);
AABB* b = reinterpret_cast<AABB*>(m->B);
//... you should change a. to a->, b. to b->
}
뒤에서 다루겠지만, A와 B의 type이 다른 경우 (예: AABB_to_Circle) A와 B가 엇갈리게 들어오는 경우가 있습니다. (예: A = Circle, B = AABB)
이러한 경우에 Circle_to_AABB를 구현하는 것은 중복된 함수를 두 개 만드는 것이 되므로, swap을 통해 해결하도록 합시다.
bool Circle_to_AABB(Manifold* m)
{
swap(m->A, m->B);
bool ret = AABB_to_Circle(m);
m->normal = -m->normal; //you should flip
swap(m->A, m->B); //re-swap
return ret;
}
2. Circle
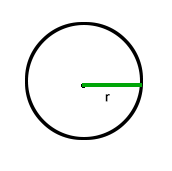
struct Circle : public Shape
{
Vec2 position;
double radius;
};원 또한 간단합니다. 코드로 따지면 되려 AABB보다 더 간단할 겁니다.
원의 정의 자체가 중심으로부터 거리가 같은 점의 집합이므로,
충돌을 판단하려는 도형에서 원과 가장 가까운 점과 원의 중심 사이의 거리를 구해, 이 값이 반지름 r보다 크다면 만나지 않는 것이고 이하라면 만나는 것이 됩니다.
원과 원의 충돌 또한 이 성질을 이용하면 됩니다.
bool Circle_to_Circle(Circle a, Circle b)
{
Vec2 n = b.position - a.position;
double r = a.radius + b.radius;
double d = n.x * n.x + n.y * n.y; //length squared
if (d > r * r) return false;
return true;
}sqrt는 연산이 비싸기 때문에, 값 자체가 필요한 것이 아니라면 제곱을 비교하도록 합시다.
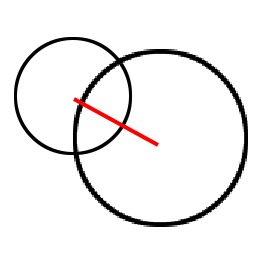
이제 Manifold를 계산해봅시다.
AABB에서와 마찬가지로 충돌의 크기는 겹친 정도, 즉 두 원의 반지름 합 - 두 중심 사이의 거리가 됩니다.
충돌의 방향은 두 원의 중심의 차와 방향이 같습니다.
충돌 지점은 원의 중심에서 충돌 방향 * 원의 반지름 만큼 이동한 지점이 됩니다.
당연히, 이 점은 원 위에 존재합니다.
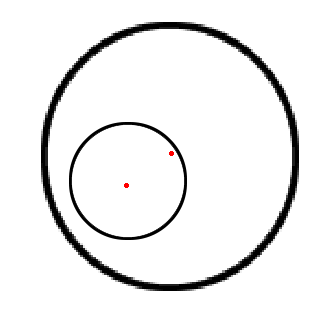
원이 포함되는 경우에도, 충돌의 크기는 (작은 원이 접할 때까지 밀어내야 하는 거리) + 2 * 작은 원의 반지름
= 큰 원의 반지름 - (두 중심 사이의 거리 + 작은 원의 반지름) + 2 * 작은 원의 반지름
= 큰 원의 반지름 + 작은 원의 반지름 - 두 중심 사이의 거리 이므로,
위에서 구한 충돌의 크기 (두 원의 반지름 합 - 두 중심 사이의 거리)와 같습니다. 충돌 방향 또한 동일합니다.
다만 두 원의 중심이 같은 경우에는 처리가 조금 다릅니다.
원을 어느 방향으로든 밀어낼 수 있고, 단위 벡터를 만들 때 사용하는 두 중심 사이의 거리가 0이므로
division by zero 문제가 발생하게 됩니다.
이러한 경우는 예외로 두고, 방향은 임의로 잡으면 됩니다.
*** reference에서는 충돌 지점을 원의 중심으로, 충돌 크기는 원의 반지름으로 하더군요.
왜 그런지는 이해하지 못했습니다.
저는 두 원의 반지름 합으로 하려다가 충돌 지점 계산이 이상해지길래 그만뒀습니다.
bool Circle_to_Circle(Manifold* m)
{
Circle* a = reinterpret_cast<Circle*>(m->A);
Circle* b = reinterpret_cast<Circle*>(m->B);
Vec2 n = b->position - a->position;
double r = a->radius + b->radius;
double d = n.x * n.x + n.y * n.y;
m->contact_count = 0;
if (d > r * r) return false;
d = sqrt(d);
m->contact_count = 1;
if (d != 0)
{
m->penetration = r - d;
m->normal = n / d;
m->contact_points[0] = a->position + m->normal * a->radius;
}
else
{
m->penetration = a->radius;
m->normal = Vec2(1, 0);
m->contact_points[0] = a->position;
}
return true;
}
3. Polygon
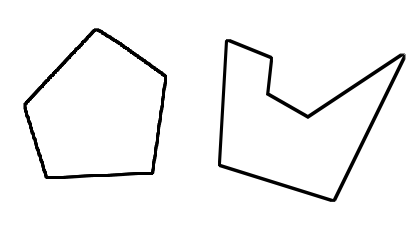
보통 Polygon이라 하면 볼록 다각형(Convex)와 오목 다각형(Concave) 둘 다 지칭하지만, 여기서는 Convex만을 다룹니다.
Concave는 처리하기가 복잡하기 때문에 Part 2에서 다루겠습니다.
Convex의 충돌 처리를 위해서는 분리축 이론 (Separating Axis Theorem, 이하 SAT)이 필요합니다.
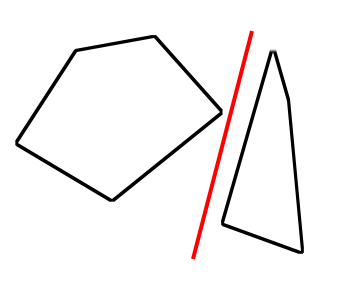
SAT는, 쉽게 말해서 어떤 선 위로 두 도형을 투영시켰을 때 만들 수 있는 두 투영 구간이 겹치지 않는다면, 두 도형은 만나지 않음을 의미한다는 것입니다. 두 도형이 만나지 않는다면 두 도형을 분리시킬 수 있는 축 하나를 그 사이에 그을 수 있다는 정도로 이해해도 괜찮을 것 같습니다.
이를 통해 충돌을 판단하기 위해서는 여러 개의 축 위로 투영시킬 필요가 있고, 여기에 각 도형의 법선 벡터 (normal vector)들을 주로 사용합니다.
따라서 Polygon을 그 도형을 이루는 각 꼭짓점과, 그 꼭짓점(에 대한 선분)에 대응되는 normal vector의 집합으로 표현할 필요가 있습니다.
const unsigned int MAX_POLY = 64; //max vertice size
struct Polygon : public Shape
{
unsigned int vertexCount;
Vec2 vertices[MAX_POLY];
Vec2 normals[MAX_POLY];
};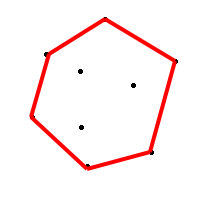
다각형을 구성하는 점들의 집합이 주어졌을 때, 여기서 Convex를 구성하고 normal을 계산할 필요도 있습니다.
점은 주로 반시계 방향 (counter-clockwise)으로 구성합니다만, 크게 상관은 없습니다. 일관성만 유지해주세요.
여기서는 reference가 시계 방향으로 정렬하는 관계로, 시계 방향을 전제로 하겠습니다.
자세한 알고리즘은 볼록 껍질(Convex Hull)에 대해 알아보시면 좋습니다.
reference의 코드를 그대로 사용할 것이므로, 벡터와 관련하여 자주 쓸 몇 가지 메서드를 미리 정의해놓겠습니다.
double Vec2::LengthSquared() const
{
return x*x + y*y;
}
double Vec2::Length() const
{
return sqrt(LengthSquared());
}
void Vec2::Normalize()
{
double d = Length();
if (d != 0)
{
x /= d;
y /= d;
}
}
double DotProduct(Vec2 a, Vec2 b)
{
return a.x * b.x + a.y * b.y;
}
double CrossProduct(Vec2 a, Vec2 b)
{
return a.x * b.y - a.y * b.x;
}
void Polygon::Set(Vec2* v, unsigned int count)
{
assert(count > 2);
count = min((int)count, MAX_POLY);
int rightMost = 0;
double highestX = v[0].x;
for (unsigned int i = 1; i < count; i++)
{
double x = v[i].x;
if (x > highestX)
{
highestX = x;
rightMost = i;
}
else if (x == highestX)
if (v[i].y < v[rightMost].y)
rightMost = i;
}
int hull[MAX_POLY];
int outCount = 0;
int indexHull = rightMost;
while (true)
{
hull[outCount] = indexHull;
int nextHullIndex = 0;
for (unsigned int i = 1; i < count; i++)
{
if (nextHullIndex == indexHull)
{
nextHullIndex = i;
continue;
}
Vec2 e1 = v[nextHullIndex] - v[hull[outCount]];
Vec2 e2 = v[i] - v[hull[outCount]];
double c = CrossProduct(e1, e2);
if (c < 0)
nextHullIndex = i;
if (c == 0 && e2.LengthSquared() > e1.LengthSquared())
nextHullIndex = i;
}
outCount++;
indexHull = nextHullIndex;
if (nextHullIndex == rightMost)
{
vertexCount = outCount;
break;
}
}
for (unsigned int i = 0; i < vertexCount; i++)
vertices[i] = v[hull[i]];
for (unsigned int i = 0; i < vertexCount; i++)
{
unsigned int i2 = i + 1 < vertexCount ? i + 1 : 0;
Vec2 face = vertices[i2] - vertices[i];
assert(face.LengthSquared() > 1e-8);
normals[i] = Vec2(face.y, -face.x);
normals[i].Normalize();
}
}
우상단에 있는 점을 찾고, 그 점을 기준으로 Convex hull point를 찾습니다.
이 방법 말고 으레 PS에서 사용하는 graham scan을 구현해서 돌려봤었는데, 뭔가 빼먹었는지 잘 작동이 안되더군요.
normal vector는 각 선분의 벡터 V를 구했을 때, (V.y, -V.x)와 뱡항이 같거나 정반대입니다.
혹시나 Polygon에 Box를 할당하고 싶다면, 네 꼭짓점을 만들어서 Set 함수를 실행해도 되겠지만
다음과 같은 함수를 구현해줘도 괜찮습니다.
void Polygon::SetBox(double w, double h)
{
vertexCount = 4;
vertices[0] = Vec2(-w / 2, -h / 2);
vertices[1] = Vec2(w / 2, -h / 2);
vertices[2] = Vec2(w / 2, h / 2);
vertices[3] = Vec2(-w / 2, h / 2);
normals[0] = Vec2(0, -1);
normals[1] = Vec2(1, 0);
normals[2] = Vec2(0, 1);
normals[3] = Vec2(-1, 0);
}Set이든 SetBox이든, 순서에 맞게 꼭짓점 및 normal vector를 매칭시켜주세요.
3-1. Transformation
다른 도형이나 Polygon이나 Translation, Scale은 공통적으로 적용될 수 있는 Transformation이고, 그 구현도 쉽습니다.
다만 Polygon은 Rotation도 적용 가능한데 (AABB는 정의 상 불가능하고, Circle은 의미가 없습니다)
이를 위해서 2D Transform Matrix를 정의해두는 것이 좋습니다.
struct Matrix_33
{
double m[3][3];
Matrix_33(double m00, double m01, double m02, double m10, double m11, double m12, double m20, double m21, double m22)
{
m[0][0] = m00;
m[0][1] = m01;
m[0][2] = m02;
m[1][0] = m10;
m[1][1] = m11;
m[1][2] = m12;
m[2][0] = m20;
m[2][1] = m21;
m[2][2] = m22;
}
void Translate(Vec2 p)
{
m[0][2] += p.x;
m[1][2] += p.y;
}
void Scale(double k)
{
m[0][0] *= k;
m[1][1] *= k;
}
void Rotate(double deg)
{
double cos = cos(deg * PI / 180);
double sin = sin(deg * PI / 180);
*this *= Matrix_33(cos, -sin, 0, sin, cos, 0, 0, 0, 0);
}
};행렬 곱셈 연산자 등의 정의는 생략했습니다.
도형을 구성하는 좌표에 행렬을 곱하면 Transformation이 적용됩니다만, 그냥 곱하면 원점을 기준으로 적용되므로 원하는 기준점이 있는 경우엔 그 기준대로 모델 공간을 변환시켜줄 필요가 있습니다.
예를 들어 Polygon의 중심점을 기준으로 Rotation을 적용하고 싶다면 다음과 같이 코드를 작성하면 됩니다.
Vec2 Polygon::GetCenter()
{
Vec2 center;
for (unsigned int i = 0; i < vertexCount; i++)
center += vertices[i];
center /= vertexCount;
return center;
}
void Polygon::Transform(Matrix_33 matrix)
{
Vec2 pivot = GetCenter();
for (unsigned int i = 0; i < vertexCount; i++)
{
vertices[i] -= pivot;
vertices[i] = matrix * vertices[i];
vertices[i] += pivot;
normals[i] = Vec2(matrix.m[0][0] * normals[i].x + matrix.m[0][1] * normals[i].y, matrix.m[1][0] * normals[i].x + matrix.m[1][1] * normals[i].y);
normals[i].Normalize();
}
}Transformation에 관한 자세한 코드는 생략하겠습니다.
Polygon 사이의 충돌 판정은 좀 복잡해 보일 수 있습니다.
앞서 말한 분리축 이론을 사용하는데, 모든 선분 쌍에 대해서 투영 구간이 겹치는 지 확인해봐야 됩니다.
A에 대한 B, B에 대한 A의 경우로 각각 나눠서 다뤄봅시다.
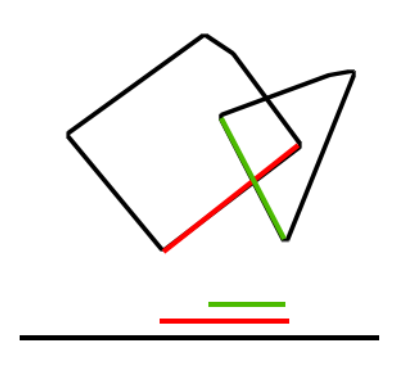
지금 우리가 검사를 위해 사용할 투영 축 벡터를 d라고 합시다. d는 기준이 되는 Polygon 상의 선분의 normal vector 중 하나가 될 겁니다. 기준이 되는 Polygon을 A, 그 나머지를 B라고 합시다.
벡터 d 상에 투영된 두 Polygon이 겹친다면, 벡터 d 상으로 투영되는 B의 꼭짓점 중 가장 가까운 점에 대해서도 성립할 겁니다.
이 점은, 다시 말하면 벡터 d와의 내적 값이 최소가 되는 B 위의 점이며 -d와의 내적 값이 최대가 되는 점이기도 합니다.
내적 값이 최대가 되는 점인 Supporting point를 구하는 함수를 미리 작성해둡시다.
Vec2 GetSupport(Vec2 dir, Vec2* vertices, unsigned int n)
{
double bestProjection = -DBL_MAX;
Vec2 bestVertex;
for (unsigned int i = 0; i < n; i++)
{
Vec2 v = vertices[i];
double projection = DotProduct(v, dir); //v.x * dir.x + v.y * dir.y
if (projection > bestProjection)
{
bestVertex = v;
bestProjection = projection;
}
}
return bestVertex;
}
이렇게 하여, A 위의 점 (normal vector인 d에 대응되는 점)에서 supporting point로 가는 벡터 (supporting point - a)와 d의 내적 값을 비교해봅시다.
support_point - a를 쓰는 것은, 다시 말하면 A의 모델 공간으로 변환하여 쓰겠다는 말이기도 합니다.
꼭짓점 a를 원점으로 하는 공간 위인 셈이니까요.
*** RandyGaul의 tutorial에서는 B의 model space라고 이야기합니다만... 제가 보기엔 A인 것 같습니다.
혹시라도 이 글을 보시는 분 중에, 제가 잘못 알고 있다면 지적해주시면 감사하겠습니다.
만약 두 Polygon이 겹치지 않는다면, A의 모델 공간 기준으로 계산되는 내적 값은 양수입니다.
겹친다면 두 벡터의 방향이 서로 가로지를 것이란 것을 (따라서 음수일 것이라는 것을) 직관적으로 알 수 있습니다.
계산되는 값 중 최댓값을 구했을 때, 이 값이 양수라면 두 Polygon은 분리축이 존재하고 (충돌하지 않고)
음수라면 분리축이 존재하지 않음을 알 수 있습니다.
정리하면, 다음과 같이 코드를 작성할 수 있습니다.
double FindAxisLeastPenetration(unsigned int* faceIndex, Vec2* a, Vec2* normals, unsigned int n, Vec2* b, unsigned int m)
{
double bestDistance = -DBL_MAX;
unsigned int bestIndex = 0;
for (unsigned int i = 0; i < n; i++)
{
double d = DotProduct(normals[i], GetSupport(-normals[i], b, m) - a[i]);
if (d > bestDistance)
{
bestDistance = d;
bestIndex = i;
}
}
*faceIndex = bestIndex;
return bestDistance;
}parameter에 대해 설명하자면,
faceIndex는 penetration이 가장 작은 A의 vertex index입니다. 후술할 때 필요합니다.
a는 A의 vertices를 , normals는 A의 normals를 의미합니다. (당연히 둘은 서로 대응되는 순서여야 합니다)
n은 A의 vertices/normals의 갯수입니다.
b는 B의 vertices를 말하고, m은 B의 vertices의 갯수입니다.
reference의 코드는 Polygon을 기준으로 작성된 반면에 제 코드는 일일이 vertex array를 가져오게 설계했는데,
후에 AABB 등과도 충돌 검사를 할 것을 감안해서 좀 더 유연하게 하기 위해서였습니다.
이렇게 A와 B에 대해, B와 A에 대해 총 두 번 penetration을 구하고, 두 값 모두 양수라면, (엄밀히 말하면, 0 이상이면 입니다) A와 B는 충돌하지 않는다는 것을 알 수 있습니다.
아직 조금 더 할 일이 있습니다.
우선, 둘 중에 더 얕은 penetration (더 큰 값이 되겠네요)을 찾고 이에 따라 기준이 될 Polygon을 골라줘야 합니다.
여기서 기준이 되는 Polygon을 ref, 그 나머지인 입사되는 Polygon을 inc라고 하겠습니다.
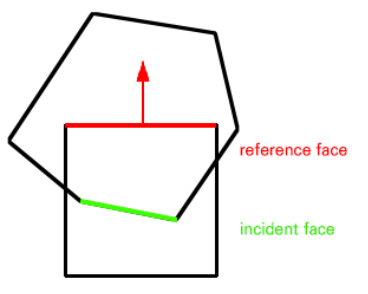
Manifold에서 실제 충돌 지점과 penetration을 구하기 위해서는, (위에서 구한 값은 normal vector에 투영된 값입니다)
충돌하는 면 (2D니까 선분이 됩니다)부터 구할 필요가 있습니다.
방금 투영된 penetration이 가장 작은 vertex index를 찾아 faceIndex에 저장해놨으니, ref 위의 faceIndex번째 꼭짓점을 기준으로 합시다. 이 점에 대응되는 normal vector를 refNormal이라고 하겠습니다.
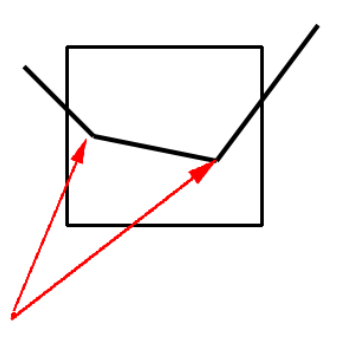
refNormal을 기준으로, inc의 모든 선분을 비교할 필요가 있습니다. 비교를 위해서는, 각 선분의 normal vector를 사용합니다.
위 그림에서 충돌하는 선분들의 내적 값은 음수이며, manifold에 계산할 때 필요한 선분의 normal vector는 refNormal과 가능한 반대 방향을 향하고 있음을 알 수 있습니다. 따라서 내적 값이 가장 작은 normal vector에 대응되는 선분이 incident face가 됩니다.
reference face는 ref에서 faceIndex번째 ~ faceIndex+1번째 꼭짓점을 잇는 선분이 됩니다.
void FindIncidentFace(Vec2* v, Vec2 refNormal, Vec2* incVertices, Vec2* incNormals, unsigned int n)
{
int incidentFace = 0;
double minDot = DBL_MAX;
for (unsigned int i = 0; i < n; i++)
{
double dot = DotProduct(refNormal, incNormals[i]);
if (dot < minDot)
{
minDot = dot;
incidentFace = i;
}
}
v[0] = incVertices[incidentFace];
incidentFace = incidentFace + 1 < n ? incidentFace + 1 : 0;
v[1] = incVertices[incidentFace];
}v에 incident face가 되는 선분의 두 꼭짓점을 저장합니다.
incVertices는 inc의 vertices를, incNormals는 inc의 normals를 의미합니다.
n은 incVertices와 incNormals의 개수입니다.
충돌 지점을 구하기 위해서 Clipping이라는 과정을 거칩니다...만
이해하기도 복잡하고, 머리를 맴도는 걸 글로 표현하기도 어렵네요.
구체적인 것은 생략하고, reference face의 두 끝점부터 시작해서 충돌 지점을 구해나간다고 이해하시면 될 것 같습니다.
충돌 지점은 Polygon 내부에 존재할 것이고, 두 끝점은 Polygon 내부로 판정할 수 있는 최소, 최대 지점이라고 볼 수 있으니 적당한 축에 투영한 값 (다시 말해 내적 값)이 그 사이에 있다면, 해당 점을 충돌 지점으로 고려할 수 있습니다.
밑의 코드에서는 기준 값을 빼서 음수이면 그런 것으로 판정하고 있습니다.
만약 두 점 중 하나만 해당된다면 선분의 일부가 내부에 포함됨을 의미합니다.
이 때는 비례식을 이용해 다른 한 점을 구해줘야 합니다.
음... 이젠 뭘 이야기하고 있는 건지도 잘 모르겠네요. 코드로 넘어갑시다.
int Clip(Vec2 n, double c, Vec2* face)
{
unsigned int sp = 0;
Vec2 out[2] = { face[0], face[1] };
double d1 = DotProduct(n, face[0]) - c;
double d2 = DotProduct(n, face[1]) - c;
if (d1 <= 0) out[sp++] = face[0];
if (d2 <= 0) out[sp++] = face[1];
if (d1 * d2 < 0)
{
double alpha = d1 / (d1 - d2);
out[sp++] = face[0] + alpha * (face[1] - face[0]);
}
face[0] = out[0];
face[1] = out[1];
assert(sp != 3);
return sp;
}
이를 활용하는 전체 코드는 다음과 같습니다.
bool Polygon_to_Polygon(Polygon a, Polygon b)
{
unsigned int temp;
double penetrationA = FindAxisLeastPenetration(&temp, a.vertices, a.normals, a.vertexCount, b.vertices, b.vertexCount);
if (penetrationA >= 0)
return false;
double penetrationB = FindAxisLeastPenetration(&temp, b.vertices, b.normals, b.vertexCount, a.vertices, a.vertexCount);
if (penetrationB >= 0)
return false;
return true;
}Manifold를 계산하지 않는다면 코드는 간단합니다.
*** 근데 이거 맞는 거겠죠? 다음 코드에서 추가되는 파트를 보면 true/false 검증을 두 번 더하는데, 이게 필요한 예외 케이스가 존재하는 건지 원본 소스 코드가 괜히 더 깐깐한건지 잘 모르겠네요. 여기서는 후자로 생각하긴 했습니다만...
bool Polygon_to_Polygon(Manifold* m)
{
Polygon* a = reinterpret_cast<Polygon*>(m->A);
Polygon* b = reinterpret_cast<Polygon*>(m->B);
unsigned int faceA;
double penetrationA = FindAxisLeastPenetration(&faceA, a->vertices, a->normals, a->vertexCount, b->vertices, b->vertexCount);
if (penetrationA >= 0)
return false;
unsigned int faceB;
double penetrationB = FindAxisLeastPenetration(&faceB, b->vertices, b->normals, b->vertexCount, a->vertices, a->vertexCount);
if (penetrationB >= 0)
return false;
unsigned int referenceIndex;
Polygon* ref, * inc;
bool flip;
if (penetrationA >= penetrationB)
{
ref = a;
inc = b;
referenceIndex = faceA;
flip = false;
}
else
{
ref = b;
inc = a;
referenceIndex = faceB;
flip = true;
}
Vec2 incidentFace[2];
FindIncidentFace(incidentFace, ref->normals[referenceIndex], inc->vertices, inc->normals, inc->vertexCount);
Vec2 v1 = ref->vertices[referenceIndex];
referenceIndex = referenceIndex + 1 == ref->vertexCount ? 0 : referenceIndex + 1;
Vec2 v2 = ref->vertices[referenceIndex];
Vec2 sidePlaneNormal = v2 - v1;
sidePlaneNormal.Normalize();
Vec2 refFaceNormal(sidePlaneNormal.y, -sidePlaneNormal.x);
double refC = DotProduct(refFaceNormal, v1);
double negSide = -DotProduct(sidePlaneNormal, v1);
double posSide = DotProduct(sidePlaneNormal, v2);
if (Clip(-sidePlaneNormal, negSide, incidentFace) < 2)
return false;
if (Clip(sidePlaneNormal, posSide, incidentFace) < 2)
return false;
m->normal = flip ? -refFaceNormal : refFaceNormal;
unsigned int cp = 0;
double separation = DotProduct(refFaceNormal, incidentFace[0]) - refC;
if (separation <= 0)
{
m->contact_points[cp] = incidentFace[0];
m->penetration = -separation;
cp++;
}
else
m->penetration = 0;
separation = DotProduct(refFaceNormal, incidentFace[1]) - refC;
if (separation <= 0)
{
m->contact_points[cp] = incidentFace[1];
m->penetration += -separation;
cp++;
m->penetration /= cp;
}
m->contact_count = cp;
return m->contact_count > 0;
}
4. Other Collisions
여기서는 방금까지 설명한 AABB, Circle, Polygon에 대한 모든 Collision Detection을 다룹니다.
이미 글이 너무 길어졌기 때문에, 각 경우에 대한 검사 방법만 서술하겠습니다.
자세한 코드는 맨 위에 링크한 reference github을 참고해주시면 감사하겠습니다.
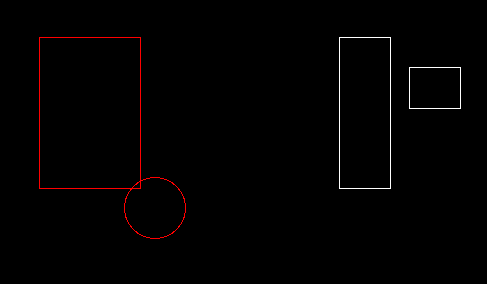
AABB - Circle : AABB에서 Circle에 가장 가까운 점을 찾고, 그 점과 Circle의 중심 사이의 거리를 비교해서 반지름 r보다 작으면 충돌하고, 크면 충돌하지 않음을 알 수 있습니다.
AABB의 중심으로부터 AABB 상의 점까지의 거리로 가능한 범위는 [-width/2 ~ width/2], [-height/2 ~ height/2] 입니다.
AABB의 중심에서 Circle의 중심으로 가는 벡터 (a)의 좌표값 크기를 해당 범위 내로 압축시키면 (Clamp하면)
AABB의 중심에서 Circle의 중심과 가장 가까운 지점까지 가는 벡터 (b)가 됩니다.
이제 b - a의 크기가 반지름 r보다 큰지 판단해주면 됩니다.
AABB - Polygon : AABB는 Polygon에 포함되므로, AABB의 네 꼭짓점과 그에 대응되는 normal vector를 구한 뒤에
Polygon - Polygon과 똑같이 처리해주면 됩니다.
Circle - Polygon : Polygon - Polygon과 비슷하게, Circle과 가장 가까운 Polygon의 face를 찾고 계산한다고 합니다.
사실 전 이해 못했습니다. 보로노이 다이어그램 이야기가 나오던데, 음... 글쎄요.
뭐... 아무튼 간에 Part 1은 여기까지 쓰겠습니다.
쓰는 데 일주일이 걸렸습니다. 중간에 정신적으로든 신체적으로든 많이 힘들고 아팠어서....
그래서 그런지 후반부는 대충 날려 쓰게 됐네요.
Part 2는 조금 쉬었다가 이어서 쓰겠습니다. 곧바로 포스팅을 할지, 아니면 이것도 시간이 좀 걸릴 지 잘 모르겠습니다.
Part 2에서는 Part 1에서 정의한 도형들을 이용해서 RoundRect, Concave를 만들어보겠습니다.
'C++ > Game' 카테고리의 다른 글
| [게임 프레임워크 개발 일지] #6 SFML의 버튼 GUI와 죽이고픈 마우스 이벤트 (0) | 2022.05.15 |
|---|---|
| [Physics] 2D 충돌 감지 구현하기 (2D Collision Detection) - Part 2 (0) | 2022.04.10 |
| [게임 프레임워크 개발 일지] #5 Multi Style이 적용된 Text (0) | 2022.02.18 |
| [게임 프레임워크 개발 일지] #4 Entity와 Component (0) | 2022.02.06 |
| [게임 프레임워크 개발 일지] #3 EventManager 설계 (0) | 2021.12.31 |