지난 번에 이어, Part 2입니다.
기본적인 구성 요소는 Part 1에서 모두 구현했기 때문에, 이번에 다룰 내용은 Part 1의 간단한 응용에 지나지 않습니다.
1. RoundRect

모서리가 둥근 사각형을 구현하기 위해서는 우리가 잘 아는, 이미 정의된 도형들로 Decomposition을 해줄 필요가 있습니다.
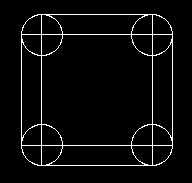
오늘 다룰 두 가지 도형들은 모두 이렇게 decomposition이 필요합니다.
RoundRect같은 경우에는 이 과정이 매우 간단한 편에 속합니다.
사각형의 width와 height, 네 귀퉁이에 그릴 원의 반지름 r은 사용자가 결정하게끔 해줍시다.
전체 너비 및 높이의 합이 width + r, height + r이 되도록 속성을 분리해줘도 좋고,
전체 너비 및 높이를 width, height으로 하고 그 중 길이 r만큼을 원을 그리는 데 따로 쓰도록 구현해도 좋습니다.
다만, 후자의 경우에는 반지름 r의 합이 width 및 height을 넘지 않도록 유의해야 합니다.
생성된 도형 집합이 원과 사각형으로, 타입이 여러 개입니다.
Part 1에서 Base Abstract Class로 Shape을 정의했으니, 동적 할당하여 Shape*로 반환하게끔 하겠습니다.
다시 downcasting이 필요할 때를 대비해 각 Derived Class마다 무슨 도형이었는지 타입을 저장하게 구현하면 좋습니다.
vector<Shape*> createRoundRect(double w, double h, double r)
{
vector<Shape*> ret;
if (r == 0)
{
ret.push_back(new AABB(Vec2(-w / 2, -h / 2), Vec2(w / 2, h / 2)));
return ret;
}
if (w / 2 <= r && h / 2 <= r)
{
ret.push_back(new Circle(r));
return ret;
}
else if (w / 2 <= r)
{
Circle* r1 = new Circle(r);
r1->position = Vec2(0, r - h / 2);
AABB* box = new AABB(Vec2(-r, r - h / 2), Vec2(r, h / 2 - r));
Circle* r2 = new Circle(r);
r2->position = Vec2(0, h / 2 - r);
ret.push_back(r1);
ret.push_back(box);
ret.push_back(r2);
return ret;
}
else if (h / 2 <= r)
{
Circle* r1 = new Circle(r);
r1->position = Vec2(r - w / 2, 0);
AABB* box = new AABB(Vec2(r - w / 2, -r), Vec2(w / 2 - r, r));
Circle* r2 = new Circle(r);
r2->position = Vec2(w / 2 - r, 0);
ret.push_back(r1);
ret.push_back(box);
ret.push_back(r2);
return ret;
}
else
{
Circle* r1 = new Circle(r);
r1->position = Vec2(r - w / 2, r - h / 2);
Circle* r2 = new Circle(r);
r2->position = Vec2(w / 2 - r, r - h / 2);
AABB* box1 = new AABB(Vec2(r - w / 2, -h / 2), Vec2(w / 2 - r, h / 2));
AABB* box2 = new AABB(Vec2(-w / 2, r - h / 2), Vec2(w / 2, h / 2 - r));
Circle* r3 = new Circle(r);
r3->position = Vec2(w / 2 - r, h / 2 - r);
Circle* r4 = new Circle(r);
r4->position = Vec2(r - w / 2, h / 2 - r);
ret.push_back(r1);
ret.push_back(r2);
ret.push_back(box1);
ret.push_back(box2);
ret.push_back(r3);
ret.push_back(r4);
return ret;
}
}단순히 각 도형들을 생성하고 vector에 넣어 반환합니다.
여기서 구현된 방법은 전체 너비 및 높이가 width, height이 되도록 하는 것이므로 각 경우에 대한 예외 처리가 앞부분에 존재합니다. (r이 0인 경우, r의 합이 width, height보다 커지는 경우)
도형을 넣는 순서는 상관없지만, 저는 외곽선을 그리기 위해서 시계 방향으로 순서를 통일했습니다.
1-1. Usage
단순히 원과 사각형 그룹을 구현한 것이기도 하고, RoundRect는 굳이 구현해서 쓰는 게 드뭅니다.
그럼에도 여기서는 구현한 이유가, 게임 내의 벽 처리 문제 때문이었습니다.

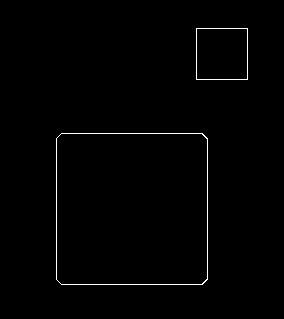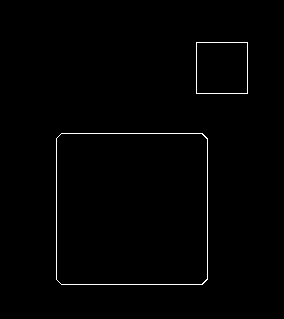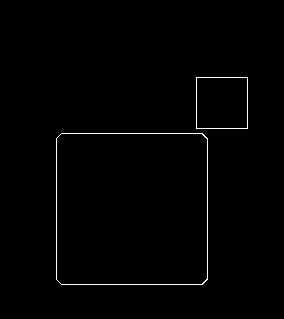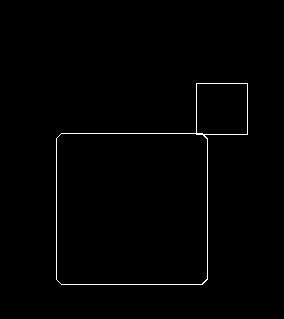
위 그림에서처럼, 플레이어가 방에 들어가기 위해 문을 열고 들어가는 경우를 생각해봅시다.
정교한 물리 엔진을 적용하면 모르겠으나 일반적인 벽 충돌 판정을 사용한다면 벽의 한가운데든 벽의 끝자락이든 동일하게 플레이어를 반대쪽으로 밀어낼 겁니다.
벽의 끝자락이 문제가 되는데, 겨우 몇 픽셀 차이로 사용자가 벽에 충돌했다고 판정하여 길을 못 지나가는 경우가 발생하면 플레이가 많이 불편해질 것이기 때문입니다.
이 문제를 해결하기 위해서 구현해본 것이 바로 RoundRect입니다.




여러 가지 테스트 케이스를 만들어서 실험해봤습니다.
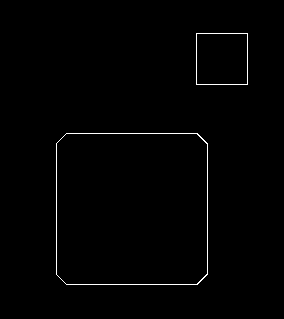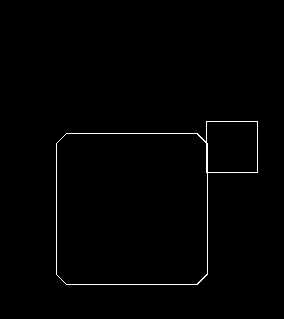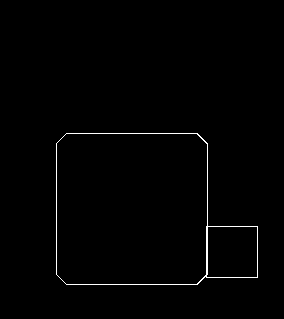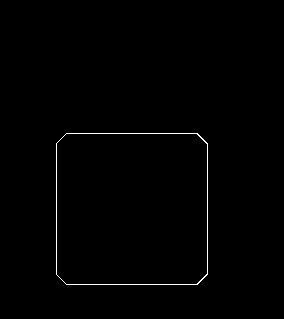
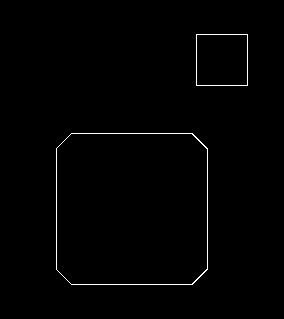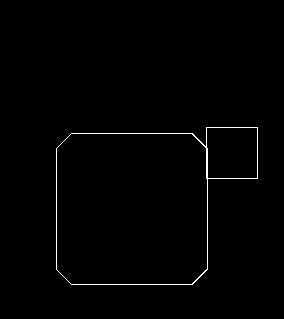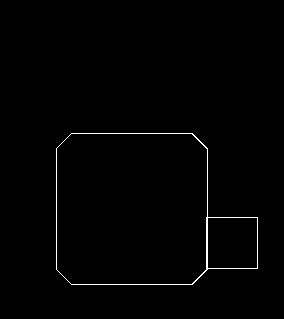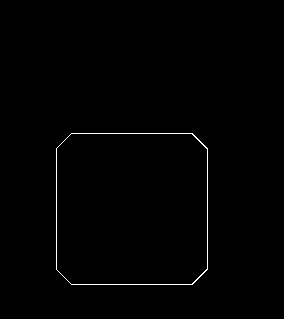
기본적으로 플레이어의 크기는 50px에, 벽과는 10px 겹치도록 했습니다.
순서대로 원의 크기가 0px (일반 사각형), 10px, 15px, 25px일 때입니다.
원의 크기가 10px 이하인 경우에는 모서리가 걸려서 사각형이 지나가지 못합니다.
그 이상으로 올려줘야 사각형이 미끄러져서 지나갑니다.
큰 차이는 없지만, 저는 원 크기가 작을 수록 움직임이 깔끔해보이는 것 같네요.
플레이어가 벽을 비껴서 지나갈 수 있는 보정치를 정하고, 그보다 조금 큰 값을 원의 크기로 하는 게 좋아보입니다.
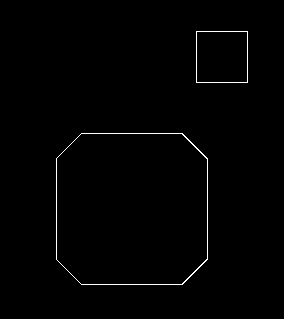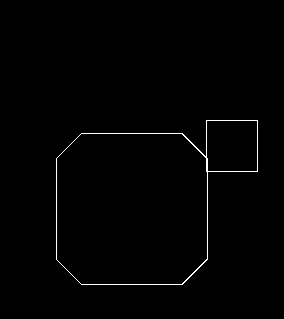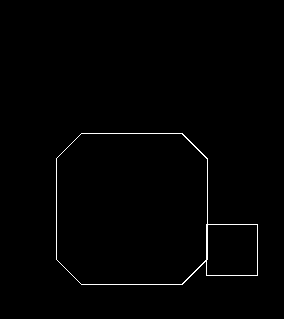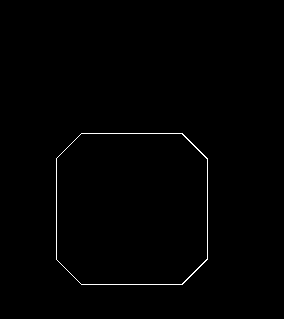
추가로 모퉁이가 45도 경사면이 되게끔 Polygon을 만들어서 실험해봤습니다.
경사면의 크기는 순서대로 5px, 10px, 15px, 25px입니다.
경사면은 10px부터 기능을 하네요.
RoundRect나 Polygon이나 크기가 작을 때는 문제가 없겠지만, 큰 경우에는 모퉁이가 안쪽으로 많이 들어가게 되어서
맵 그래픽이 사각형 형태로 그려질 것을 생각하면 모양새가 별로 안 좋게 나올 수도 있습니다.
개인적으로 생각해봤을 때, 움직임이 깔끔하게 나오는 것은 RoundRect이고 관리가 쉬운 것은 Polygon입니다.
RoundRect는 도형 하나에 최대 6개의 도형 (원 4개와 사각형 2개)이 필요하고 이를 도형이 한 개인 것처럼 관리해주는 것은 좀 번거롭습니다.
Polygon은 말그대로 Polygon인 탓에, 충돌 판정 때 연산이 좀 더 깁니다. RoundRect가 판단할 도형 수가 더 많긴 하지만, 그래도 간단한 사각형과 원일 뿐이니까요. 뭐 사실 퍼포먼스 테스트 급으로 늘려보는 게 아닌 이상 이 연산 하나로 성능이 차이날 정도는 아닐 겁니다.
2. Concave
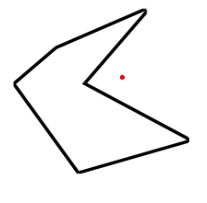
오목 다각형은 특성상 모양이 복잡합니다. 단순한 모양의 다각형으로 바꿔줄 필요가 있습니다.
가장 단순한 다각형이라면, 삼각형이 되겠죠.
서로 교차하는 선분들이 존재하는 게 아닌 이상, 다각형을 구성하는 꼭짓점만을 이용하여 다각형을 모두 채우도록 삼각형을 그릴 수 있습니다. (선분이 교차하는 경우와 구멍이 존재하는 경우도 다루고 싶었는데, 이건 알고리즘 자료도 잘 없고 난이도가 높아서 포기했습니다.)
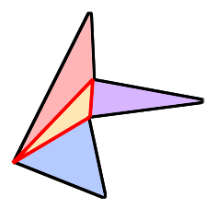
이렇게 다각형을 삼각형 집합으로 분할하는 것을 삼각분할 (triangulation)이라고 합니다.
들로네 삼각분할이 유명하지만, 여기서는 굳이 그 단계까지 가지는 않겠습니다.
여기서 사용하는 알고리즘은 Ear Clipping Algorithm입니다.
구멍이 존재하지 않는 4개 이상의 꼭짓점을 가진 다각형에 적용할 수 있습니다.
위키피디아에 의하면 구현이 간단한 대신 다른 알고리즘 대비 느리고 구멍이 있으면 안된다는 단점이 있다고 하네요.
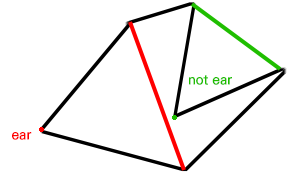
Ear Clipping Algorithm은 Two Ear Theorem (두 귀 정리)를 기반으로 합니다.
두 귀 정리란 세 개 이상의 꼭짓점이 있는 단순 다각형에는 '귀'가 적어도 두 개 이상 존재한다는 것을 의미하며,
다각형 $P$ 위의 점 $p_i$에 대해 $p_i$와 연결되는 $P$ 위의 두 꼭짓점 $p_{i-1}$와 $p_{i+1}$을 잇는 대각선이 $P$에 완전히 포함되는 경우, $p_i$를 귀라고 합니다.
꼭짓점 집합에서 이러한 귀를 찾으면서, 귀가 포함되는 삼각형을 만들고 집합에서 귀를 지우는 과정을 삼각형이 하나만 남을 때까지 반복합니다.
구현을 위해서 점이 삼각형 내부에 존재하는지 판별하는 함수가 필요합니다.
알고리즘 자체에는 필요없지만, Part 1에서 구현한 Polygon의 Set 함수 때문에 생성되는 삼각형의 꼭짓점 순서가 뒤죽박죽이 될 수 있습니다. 충돌에 문제가 생기는 건 아니지만, 외곽선을 그릴 때 문제가 됩니다.
삼각형의 edge마다 개수를 세어 1번씩만 나오는 edge를 따로 모아 그려주는 방법도 되긴 하겠으나...
연산도 복잡해지고 많이 번거롭습니다. 그래서 어차피 점 3개짜리 삼각형이라 Convex Hull을 찾을 필요가 없으니
이 과정 없이 바로 Polygon을 만들 수 있도록 SetDirect라는 함수를 구현해주겠습니다.
triangulation 함수에서 자체적으로 꼭짓점 순서를 정렬하여 삼각형을 생성하므로, 외곽선을 그리고 싶다면 삼각형을 순회하면서 나오는 순서대로 중복이 없게끔 점을 추가한 뒤에 이어주면 됩니다.
사실 애초에 다각형에 불필요한 점이 없다면, 그냥 원본 점 데이터를 갖고와서 그대로 이어주는 게 가장 편한 방법입니다.
bool InsideTriangle(Vec2 t1, Vec2 t2, Vec2 t3, Vec2 p)
{
Vec2 a = t2 - t1, b = t3 - t2, c = t1 - t3;
return (CrossProduct(a, p - t1) > 0 && CrossProduct(b, p - t2) > 0 && CrossProduct(c, p - t3) > 0);
}
void Polygon::SetDirect(Vec2* v, unsigned int count)
{
assert(count > 2);
count = min((int)count, MAX_POLY);
vertexCount = count;
for (unsigned int i = 0; i < vertexCount; i++)
vertices[i] = v[i];
for (unsigned int i = 0; i < vertexCount; i++)
{
unsigned int i2 = i + 1 < vertexCount ? i + 1 : 0;
Vec2 face = vertices[i2] - vertices[i];
assert(face.LengthSquared() > 1e-8);
normals[i] = Vec2(face.y, -face.x);
normals[i].Normalize();
}
}
vector<Shape*> triangulation(const vector<Vec2>& v)
{
if (v.size() < 3) return {};
Vec2 triangle[3];
vector<Shape*> ret;
if (v.size() == 3)
{
triangle[0] = v[0], triangle[1] = v[1], triangle[2] = v[2];
Polygon* polygon = new Polygon;
polygon->SetDirect(triangle, 3);
ret.push_back(polygon);
return ret;
}
double area = 0;
int N = v.size();
for (int i = 0; i < N; i++)
area += CrossProduct(v[(i + 1) % N], v[i]);
vector<int> idx;
if (area < 0)
for (int i = 0; i < N; i++) idx.push_back(i);
else
for (int i = 0; i < N; i++) idx.push_back(N - i - 1);
for (int j = N - 1; N > 2;)
{
int i = j % N;
j = (i + 1) % N;
int k = (j + 1) % N;
bool ear = CrossProduct(v[idx[k]] - v[idx[i]], v[idx[j]] - v[idx[i]]) < 0;
for (int t = 0; ear && t < idx.size(); t++)
if (t == i || t == j || t == k) continue;
else ear = !InsideTriangle(v[idx[i]], v[idx[j]], v[idx[k]], v[idx[t]]);
if (ear)
{
triangle[0] = v[idx[i]], triangle[1] = v[idx[j]], triangle[2] = v[idx[k]];
Polygon* polygon = new Polygon;
polygon->SetDirect(triangle, 3);
ret.push_back(polygon);
for (int t = j; t < N - 1; t++) idx[t] = idx[t + 1];
N--;
}
}
return ret;
}
3. Conclusion
지금까지 2D 충돌 감지를 구현해봤습니다.
게임 개발에 쓰려고 관련 라이브러리를 찾아보다가 너무 무겁거나 Linking error가 나서 짜증나거나 그런 탓에
그냥 내가 튜토리얼 보고 대충 만들어놓자 해서 시작했는데, 시간이 참 오래 걸렸네요.
이제 다시 다른 기능을 건드려봐야겠습니다.
아니면... 잠시 쉬면서 다른 영역을 시도해도 괜찮을 것 같네요.
천천히 생각하겠습니다.
'C++ > Game' 카테고리의 다른 글
| [게임 프레임워크 개발 일지] #7 Variadic Template과 Lambda (0) | 2022.07.20 |
|---|---|
| [게임 프레임워크 개발 일지] #6 SFML의 버튼 GUI와 죽이고픈 마우스 이벤트 (0) | 2022.05.15 |
| [Physics] 2D 충돌 감지 구현하기 (2D Collision Detection) - Part 1 (1) | 2022.04.09 |
| [게임 프레임워크 개발 일지] #5 Multi Style이 적용된 Text (0) | 2022.02.18 |
| [게임 프레임워크 개발 일지] #4 Entity와 Component (0) | 2022.02.06 |