다른 블로그 포스팅을 보면서 공부한 것을 정리한 글입니다.
Convex Hull Trick은 특정 형태의 점화식을 사용하는 다이나믹 프로그래밍을 빠르게 계산하기 위한 방법입니다.
점화식은 다음과 같습니다.
$$D_i = \min_{j < i} (D_j + A_i \times B_j ) $$
단, 여기서 $B_j$는 증가함에 따라 감소하는 값이어야 합니다. ($a < b$일 때, $B_a > B_b$)
$D_i$의 최솟값을 구하기 위해 그래프의 개형을 구해봅시다.
$i$가 같을 때는 $A_i$도 같은 값이니 $x$축을 $A_i$로 하여, $y = B_j \times x + D_j$를 그리면 다음과 같습니다.
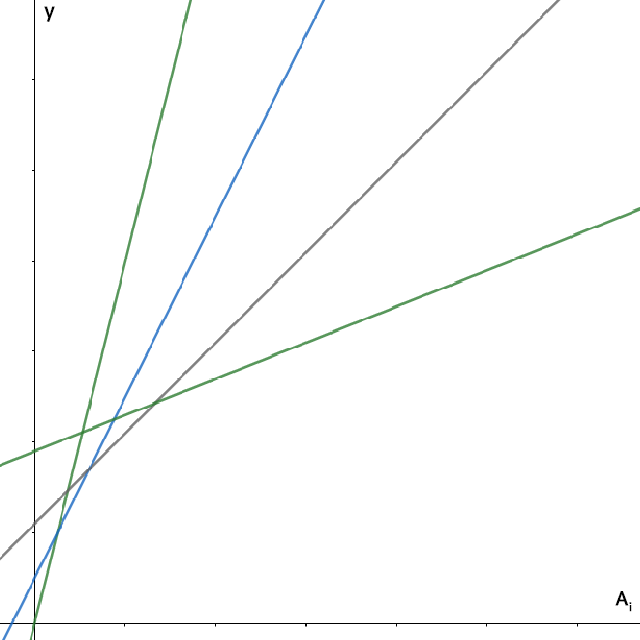
$j$가 커질 수록 직선의 기울기 $B_j$는 감소합니다.
$y$축과 만나는 점인 $(0, D_j )$는 증가할 수도 감소할 수도 있습니다.
$D_i = \min_{j < i} (D_j + A_i \times B_j ) = \min (\min_{j < i - 1} (D_j + A_{i-1} \times B_j ) , D_{i - 1} + A_i \times B_{i - 1} )$
$= \min (D_{i - 1} , D_{i - 1} + A_i \times B_{i -1} )$
에서 $A_i \times B_{i - 1}$가 양수일 수도, 음수일 수도 있기 때문입니다.
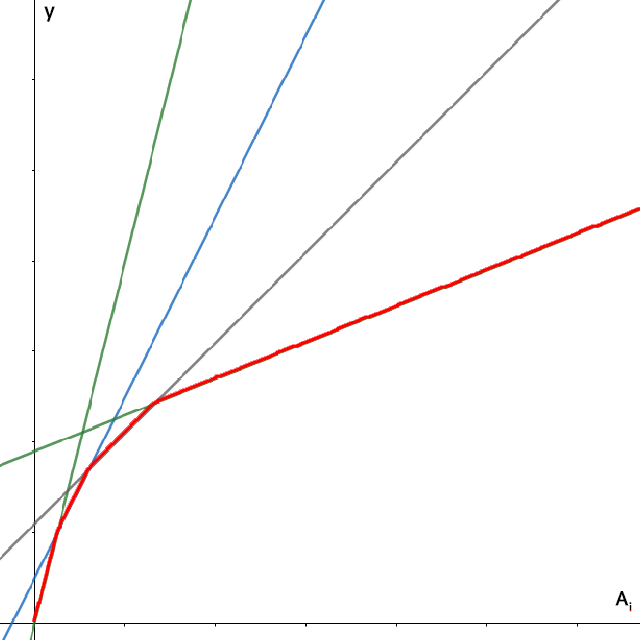
우리가 원하는 값 $D_i = \min(y)$이므로, 빨간 선 위의 값에 해당합니다.
따라서 직선마다 그 직선의 계산 값이 최솟값이 되는 구간을 계산해야 합니다.
$k$번째 직선의 방정식을 구하기 위해서는 $D_0 , ... , D_{k-1}$의 값을 모두 알아야 합니다.
그러므로 $k = 0$에서 시작하여 $k$번째 직선을 차례대로 추가하면서 최솟값을 갖는 구간을 구해야 합니다.
$k$번째 직선 ($y = B_k \times x + D_k$) 이 최솟값을 가지는 구간을 $[x_k , x_{k + 1} ]$라고 합시다.
$k$번째 직선과 $k - 1$번째 직선이 만나는 교점 $P(x_p, y_p)$에 대해
1. $x_{k-1} < x_p$인 경우, $k-1$번째 직선이 최솟값을 가지는 구간은 $[x_{k-1}, x_p]$ 이므로 $x_k = x_p$입니다.
(기울기 $B_k < B_{k-1}$이므로 교점 $P$ 이후로는 이전 직선이 더 작은 값을 가지는 경우는 없습니다)

2. $x_p \le x_{k -1}$인 경우, $k$번째 직선이 추가된 이후로 $k - 1$번째 직선이 최솟값을 가지는 구간이 없어지게 됩니다. 이런 경우 $k - 1$번째 직선을 제외시키고, 그 전 직선을 가져와 과정을 반복합니다.
결과적으로, 1번 경우에서만 $x_k$를 정하고 넘어갈 수 있으므로, $x_k = x_p$로 동일합니다.

그래프에서 보이듯이 k번째 직선이 추가된 후에 k-1번째 직선이 최솟값 라인에 영향을 끼치지 못합니다.
그래서 k-1번째 직선을 지우고 그 전 직선을 가져와 다시 최솟값 구간을 갱신해주는 겁니다.

이러한 과정을 거치고 나면, 직선 리스트에는 각 직선이 최솟값을 갖는 구간이 오름차순으로 정렬되어 있게 됩니다.
$x = A_i$ 선 위의 값들 중 최솟값은 $x_k \le A_i$인 구간 중 $x_k$가 최대인 구간을 찾으면 되므로,
이분 탐색을 통해 구할 수 있습니다. $=O(\log n)$
이를 총 N개의 $D_i$를 구하기 위해 반복하므로 시간복잡도는 $O(n \log n)$입니다.
+) $A_i$가 $i$가 증가함에 따라 증가하는 경우
일반적으로는 $A_i$가 증가하는지 감소하는지 알 수 없으므로, 각 직선의 정보를 모두 저장하고 이분 탐색을 통해 최솟값을 갖는 직선을 찾아야 합니다.
그런데 $A_i$가 $i$가 증가함에 따라 증가한다면, 다음이 성립합니다.
$k$번째 직선이 최솟값을 갖는 구간 $[x_k, x_{k+1}]$에 대해 $x_k \le A_i$가 성립한다면,
$j \ge i$인 모든 $A_j$에 대해서도 $x_k \le A_j$입니다.
따라서 $D_i$를 계산할 때 $x_k \le A_i$였다면 $0 \sim k - 1$번째 직선은 고려하지 않아도 되며,
이 이후로는 다시 쓰이지 않습니다. 그러므로 이 직선들을 모두 제거할 수 있습니다.
그러므로 리스트에 남아 있는 직선 중 맨 앞의 직선만을 사용하여 값을 계산할 수 있습니다.
이러한 경우에는 이분 탐색을 사용하지 않으므로, 시간 복잡도는 $O(n)$입니다.
이러한 기법을 사용하는 대표적인 문제가 13263. 나무 자르기 입니다.
다음 글에서 이를 사용하여 문제를 풀어보겠습니다.
+) 추가
CHT는 max를 쓰는 DP에서도 사용할 수 있습니다.
min의 경우에 CHT를 쓸 수 있었던 이유는 $B_i$가 감소하는 형태이므로
다음 직선이 더 작은 값을 가진다는 것이 보장되었기 때문입니다.
그러니 max의 경우에는 $B_i$가 증가하는 형태라면 CHT를 사용할 수 있습니다.
'C++ > PS' 카테고리의 다른 글
| [BOJ/C++] 23744. 알고리즘 과외 (0) | 2022.01.05 |
|---|---|
| [BOJ/C++] 17476. 수열과 쿼리 28 (0) | 2021.12.27 |
| [BOJ/C++] 13263. 나무 자르기 (0) | 2021.12.22 |
| [BOJ/C++] 15896. &+ +& (0) | 2021.12.21 |
| [BOJ/C++] 13705. Ax+Bsin(x)=C (2) | 2021.12.20 |