다시 PS를 건드리는 일이 없을 줄 알았건만, 건드릴 일이 생겼습니다.
Slope Trick을 이용해 풀어야 하는 문제가 있었는데,
옛날에 이론을 공부할 때도 잘 이해하지 못하고 대충 그렇구나 하고 예제만 풀고 넘겼어서
이번 기회에 다시 정리해서 글로 남겨야겠다고 생각했습니다.
어떻게든 이해하겠다고 온몸 비튼 뒤에 적는 거라서 뭔가 잘못되었을 수도 있습니다.
근데 아무튼 적을 거임
사실 이제 코테 같은 거 할 생각도 없는데 이게 나에게 무슨 의미가 있을지는 모르겠습니다만...
Slope Trick은 대충 다음과 같은 형태로 나타나는 점화식 문제를 최적화하여 푸는 데 사용됩니다.
$f_1 (X) = \min \limits_{Y \le X} (|A_1 - X|)$
$f_i (X) = \min \limits _{Y \le X} (f_{i-1} (Y) + |A_i - X|))$ $, i > 1$
문제에 따라 점화식의 형태가 달라질 수 있습니다만, 골자는 비슷할 겁니다. 아마도.
위에서 제시한 형태가 가장 기본적이니, 이걸 기준으로 설명하겠습니다.
이 점화식이 나오는 상황을 문제로 비유하면,
길이가 $N$인 수열 $A$에 대해 $|A_i - B_i|$ 의 합을 최소화하는 단조 증가수열 ($B_i \le B_{i+1}$) $B$ 를 찾고
그 최소 합 $\sum\limits_{i=1}^{N} |A_i - B_i|$을 구하라고 직접 이야기하거나 ( 백준 13323 )
$A_i$를 1 올리거나 내리는 데 비용이 1이 든다고 할 때, 수열 $A$를 오름차순으로 정렬된 수열로 바꾸는 최소 비용을 구하라는 문제가 되겠습니다. ( codeforces 713C )
다시 말해서 1 3 2 4 5 를 오름차순 ($B_i \le B_{i+1}$)으로 정렬된 수열로 바꾸는 최소 비용을 묻는다면,
1 2 2 4 5 혹은 1 3 3 4 5 으로 변경하는 비용 1이라고 대답해야 하는 문제입니다.
위에서 예시로 든 두 문제에서는 여기서 조건이 더 엄격해서, $B$가 강한 증가수열 (strictly increasing, $B_i < B_{i+1}$) 이라고 명시하고 있습니다. (1 3 2 4 5 를 1 2 3 4 5으로 바꾸는 문제)
요거에 대해서는 나중에 얘기하겠습니다.
먼저 이 문제에서 어떻게 점화식을 유도하는지 봅시다.
$D_i (x)$를, $A_i$를 $x$로 변경했다고 가정할 때 $A_1$부터 $A_i$까지의 수열을 바꾸는 비용의 최솟값,
즉 $\sum\limits_{t=1}^{i} |A_t - B_t|$의 최솟값이라고 정의합시다.
그렇다면 $D_i (x)$은 [$A_1$ ~ $A_{i-1}$을 모두 $x$ 이하인 증가수열로 만드는 최소 비용] + [$A_i$를 $x$로 바꾸는 비용] 이므로,
이를 다음과 같은 점화식으로 표현할 수 있습니다.
$D_1 (x) = |A_1 - x|$
$D_i (x) = \min \limits _{t \le x} D_{i-1} (t) + |A_i - x|$ $, i > 1$
$D_1 (x)$부터 그래프로 그려봅시다.


왼쪽은 $y=D_1 (x)$ , 오른쪽은 $y=\min \limits _{t \le x} D_1 (t)$ 를 그린 그래프입니다.
이제 여기에 $A_2$를 추가해 봅시다.
1] $A_1 \le A_2$ 일 때



첫 번째 그림의 녹색 함수 + 빨간 함수가 두 번째 그림의 함수 $D_2 (x)$ 입니다.
$x=A_2$ 일 때 $D_2 (x)$ 의 값이 최소가 되며, 이 값은 0입니다.
2] $A_1 > A_2$ 일 때



여기서는 $A_2 \le x \le A_1$인 $x$라면 무엇이든 $D_2 (x)$ 의 값이 최소가 되는군요,
다만 그 값은 $A_1 - A_2$가 됩니다.
두 가지 경우에서 보이듯이, 세 번째 그림들의 $y=\min \limits _{t \le x} D_2 (t)$ 는 기울기가 0인 구간에서 최솟값을 가집니다.
각 경우의 두 번째 그림들을 보면 $y=D_2 (x)$ 는 $x$가 증가함에 따라 기울기가 증가하기 때문에 (도함수가 증가함수이기 때문에)
$y=D_2 (x)$의 기울기가 0인 구간 혹은 기울기의 부호가 양수로 바뀌는 극점에서 최솟값을 찍었다가,
기울기가 양수가 되기 때문에 더 이상 감소하지 않으므로 이 구간부터는 기울기가 0으로 유지된다고 볼 수 있겠습니다.
따라서, 이 구간의 $x$를 찾을 수 있다면, $D_i (x)$의 최솟값을 구할 수 있습니다.
함수의 기울기를 중심으로 상황을 다시 살펴봅시다.

$A_1$을 기준으로 왼쪽 함수의 기울기는 -1, 오른쪽은 1입니다.
$y = |A_1 - x|$의 구간에 따른 기울기를 한 번 적어봅시다.

$A_1$ 기준으로 왼쪽은 기울기가 -1, 오른쪽은 기울기가 1이라는 의미입니다.
그런데 이렇게 적어놓으니 기울기가 0인 구간을 알기가 어렵네요.
그러니 $A_1$을 2개 넣어서, 기울기가 0인 구간을 표현하겠습니다. 극한에서 $\lim\limits_{x \rightarrow 0-}$와 $\lim \limits_{x \rightarrow 0+}$를 쓰는 느낌이네요.

이제 다음으로 넘어갑시다.
$A_2$를 추가해야 하는데, $D_2 (x) = \min \limits_{t \le x} D_1 (x) + |A_2 - x|$이므로
$D_1 (x) = |A_1 - x|$에 $\min$을 적용하면서 기울기가 양수인 구간이 사라진다고 했었죠.
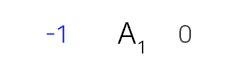
그래프로 보면 다음 그림에서 왼쪽에서 오른쪽으로 넘어간 것과 같습니다.


여기서 $A_2$를 추가합니다. ($y = |A_2 - x|$)
$A_2$가 $A_1$보다 크냐 작냐에 따라 기울기 변화가 달라지겠네요
$A_1 < A_2$인 경우부터 봅시다.

$A_2$를 기준으로 왼쪽은 기울기가 -1, 오른쪽은 기울기가 +1 됩니다.

이런 식으로 되겠네요.
$x < A_1$인 구간의 기울기가 -2,
$A_1 \le x \le A_2$인 구간의 기울기가 -1,
$A_2 < x$인 구간의 기울기가 1이라는 뜻입니다.
기울기가 0인 구간은 존재하지 않습니다.
이걸 그린 그래프가 다음과 같습니다.

$A_1 > A_2$인 경우도 볼까요


마찬가지로,
$x < A_2$인 구간의 기울기가 -2,
$A_2 \le x \le A_1$인 구간의 기울기가 0,
$A_1 < x$인 구간의 기울기가 1입니다.
기울기가 -1인 구간은 존재하지 않습니다.
이걸 그린 그래프는 다음과 같습니다.

$A_1 = A_2$인 경우에는, $A_2$를 $A_1$로 바꿔서 표현할 수 있습니다.


극점이 $x =A_1$ 하나뿐이고
$x < A_1$인 구간에서 기울기가 -2,
$x > A_1$인 구간에서 기울기가 1이군요.

$A_1$ 왼쪽의 기울기가 -2가 되었다는 것을 빼면 $y = D_1 (x)$와 개형이 똑같습니다.
$x= A_1$에서 최솟값을 가지며, 값은 0인 것도 변함없이 유지되는군요.
여기서 알 수 있는 것은


집합 $S$를 이 그림에서 보이는 $A_i$들의 집합이라고 할 때, (의미상으로는 기울기가 변하는 극점의 $x$좌표의 집합이라 볼 수 있겠네요)
기울기가 0 또는 음수에서, 양수로 바뀌는 극점의 $x = \max(S)$ (집합 $S$의 최댓값)이라는 것을 알 수 있습니다.
기울기가 증가함수이기 때문에, $x = \max(S)$의 오른쪽 구간의 기울기가 가장 크다는 것을 유추할 수 있습니다.
(위 그림에서 따지면 오른쪽으로 갈수록 기울기가 증가하니, 가장 오른쪽에 있는 값 $\max(S)$ 오른쪽 구간의 기울기가 가장 크다는 말이 되겠네요.)
그런데 매 과정마다 $\min$을 적용하면서 매번 양수인 구간을 지워버리기 때문에
$A_i$를 추가하기 전에는 가장 오른쪽 구간의 기울기가 0이고, 추가한 후에는 기울기가 1일 수밖에 없습니다.
그러니 $\max(S)$ 왼쪽에 있는 구간들의 기울기는 0 이하일 수밖에 없죠.
그리고 이 $x = \max(S)$에서 $D_i (x)$가 최소가 됩니다.
그럼 이 집합 $S$를 만드는 과정만 정리하면, $D_i (x)$의 최솟값을 구할 수 있습니다.
아까의 과정을 다시 봅시다.
$A_1$를 기준으로 왼쪽의 기울기가 -1, 오른쪽의 기울기가 +1 됩니다.
우리는 편의상 기울기가 +0되는 구간을 표시하기 위해 $A_1$를 두 번 추가했으니, 이를 반영해 줍시다.
집합 $S$에 $A_1$를 2번 추가해 줄 겁니다.
좀 더 명확히 말하면 기울기를 제대로 반영하기 위해서 2번 추가해 주는 거라고 보면 됩니다.
기울기 1과 -1 사이의 차는 1이 아니라 2이니까요..
$D_1 (x) = |A_1 - x|$ 이므로, 이를 계산하는 것은 쉽습니다.
$x = A_1$에서 최솟값 0을 계산할 수 있습니다.
그다음부터는 $D_i (x) = \min \limits _{t \le x} D_{i-1} (t) + |A_i - x|$ 에 따라 계산해야 합니다.
$\min \limits _{t \le x} D_i (t)$가 적용되면서, 기울기가 양수인 구간을 지워줬습니다.

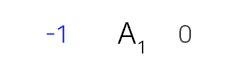
왼쪽에서 오른쪽으로 넘어갔었습니다. 그랬었죠?
아까 $x=\max(S)$에서 기울기가 양수로 바뀐다고 했으니 이 구간을 없애려면, 집합 $S$에서 $\max(S)$를 1번 제거하면 되겠네요.
$D_2 (x)$를 계산하기 위해 다시 $A_2$를 2번 추가합니다.
$D_2 (x)$는 $x=\max(S)$에서 최솟값을 가지므로, 이를 이용해 계산해 줍니다.
$D_2 (x) = 0 + |A_2 - \max(S)|$
$A_1 < A_2$인 경우 $\max(S) = A_2$이므로 여전히 최솟값이 0이고
$A_2 < A_1$인 경우 $\max(S) = A_1$이므로 최솟값이 $A_1 - A_2$로 갱신됩니다.


계산이 끝났으니 $\min$을 적용하기 위해 $S$에서 $\max(S)$를 1번 제거합니다.
이렇게 과정을 반복하면 됩니다.
$A_1 < A_2$인 경우와 $A_1 = A_2$인 경우에서 보았듯이,
$A_i \ge \max(S_{before})$인 상황이라면 최솟값이 갱신되지 않습니다.
$\min \limits _{t \le x} D_{i-1} (t)$가 최소가 되는 구간이 $x \ge \max(S_{before})$이므로, $|A_i - x| = 0$으로 최소가 되는 $x = A_i$가 이 구간에 존재하기 때문입니다.
따라서 $A_i \ge \max(S_{before})$ 라면, 이 과정을 생략하고 $A_i$를 1개만 추가하고 넘어가면 됩니다.
그렇지 않다면, $A_i$를 2개 추가하고, $\max(S_{after})$를 1번 제거합니다.
이론상으로는 조건을 따지지 않고 2개 추가 후 1번 제거하고, 그렇게 구현해도 되지만
여기서는 비용 계산이 목적이므로 최적화하는 것입니다.
이를 알고리즘으로 정리하면
0. 초기값 $i = 1, S = \{\}$
1. $A_i \ge \max(S)$인 경우, $S$에 $A_i$ 1개 추가 후 3번으로 이동
2. 그렇지 않은 경우, 다음 과정을 수행
2-1. $A_i$를 $S$에 2개 추가
2-2. $|A_i - \max(S)|$를 계산하여 $cost$에 더함
2-3. $S$에서 $\max(S)$를 1번 제거 후 3번으로 이동
3. $i$에 1을 더하고, $i = N$이 될 때까지 1번부터 과정을 반복
정도가 되겠네요. 최댓값을 사용하니 priority queue를 써서 구현하면 다음과 같은 코드가 됩니다.
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
int N, A[...];
long long ans = 0;
priority_queue<int> q;
int main()
{
... //get input to array A
for (int i = 0; i < N; i++)
{
q.push(A[i]);
if (q.top() > A[i]) //A[i] < max(S)
{
ans += abs(q.top() - A[i]);
q.push(A[i]);
q.pop();
}
}
cout << ans <<;
return 0;
}
q.top() (=$\max(S_{before})$) 과 A[i]를 먼저 비교하려 하면 priority queue가 비어있을 때 예외가 발생하므로,
일단 A[i]를 하나 추가한 뒤에 비교하게 했습니다.
대소 관계에 상관없이 A[i]가 적어도 1개는 들어가야 하며,
$A_i > \max(S_{before})$라면, $\max(S_{after}) = \max(S_{before} + \{A_i\}) = A_i$ 일 테니 $A_i$와 $max(S_{before}+ \{A_i\})$를 비교하여
$A_i$가 더 작은 경우에만 (혹은 같지 않은 경우) 과정을 마저 진행하게 만들어줬습니다.
구현은 굉장히 간단합니다.
이론이 이해하기 더럽게 어려웠어서 그렇지...
그런데, 이 $x$를 역추적해야 하는 문제도 있습니다.
다시 말해서 $\sum\limits_{i=1}^{N} |A_i - B_i|$의 최솟값을 구하는 게 아니라, 이 값이 최소가 되는 단조 증가수열 $B$를 찾으라는 문제입니다.
위 과정에서 찾아 사용했던 $x=\max(S)$와는 다릅니다.
$\min$을 적용하는 과정에서 $\max(S)$가 집합 $S$에서 제거되기 때문에,
여기서 찾은 $x$를 그대로 쓰면 $B_i \le B_{i+1}$이 성립하지 않을 수 있습니다.
그래프로 보면 다음과 같은 경우가 됩니다.

$A_2$를 추가하는 과정에서 $A_2 < A_1$이라서 $\max(S) = A_1$을 $x$로 사용한 후 $S$에서 제거했습니다.
그리고 $A_2 < A_3 < A_1$인 $A_3$을 $S$에 추가한 상황입니다.
$A_1$을 이미 사용하고 제거했으므로 집합 $S = \{A_2, A_3\}$이고, $x=\max(S)=A_3$을 이용해 최솟값을 계산할 겁니다.
네, 여기까진 문제가 없습니다. 값도 최소가 맞습니다.
그런데 이 $x$를 그대로 $B_i$에 대입하려고 보면 모순이 발생합니다.
$B_2 = A_1$인데, $B_3 = A_3$이 되기 때문에, $B_2 > B_3$이므로 단조 증가 수열이라는 조건이 성립하지 않습니다.
$A_1$이 $\min$을 적용하는 과정에서 제거되어 그 이후에 반영되지 않기 때문입니다.
그래프의 개형으로 생각하면, $x=A_1$에서 극점이 사라지고 기울기가 0으로 평평해졌기 때문에 그렇다고 볼 수 있겠네요.


따라서 최솟값이 되는 수열 $B$를 구하기 위해서는 별도의 과정이 필요합니다.
일단 아까의 알고리즘을 $i=N$까지 진행했다고 생각해 봅시다.
$D_N (x)$가 최소가 되는 $x = \max(S)$입니다.
여기서 $S$에 더 추가되어 상황을 꼬이게 만들 $A_i$가 이제는 없으니, $B_N = \max(S)$로 확정 지을 수 있습니다.
이제 여기서부터 출발해서, $B_i$를 역으로 맞춰나가야 됩니다.
좀 더 편하게 보기 위해서 $S_i$를 $D_i(x)$를 계산할 시점 ($\min$을 적용하기 전)의 집합 $S$라고 생각합시다.
$S_1 = \{A_1, A_1\}$이고, $S_i = S_{i-1} - \max(S_{i-1}) + \{A_i, A_i\}$ 입니다.
문제가 되는 경우는 아까 말했듯이, $B_i < \max(S_{i-1})$인 경우입니다.
$\max(S_{i-1}) \le B_i$라면, $B_{i-1} = \max(S_{i-1})$로 두어도 상관이 없습니다.
$B_i < \max(S_{i-1})$일 때 $D_{i-1} (x)$ 그래프의 개형을 생각해 봅시다.
$D_{i-1} (x)$는 $x < \max(S_{i-1})$ 구간에서 기울기가 0 이하, 즉 감소함수입니다.
아까도 말했듯이, $x = \max(S)$에서 기울기가 음수 또는 0에서 양수로 바뀌니까요.
바로 위 그래프를 다시 가져와 예시로 들면, $D_2 (x)$는 $x < \max(S_2) (=A_1)$에서 감소함수입니다.

따라서 $x < \max(S_{i-1})$인 구간에 속하는 $x$가 $\max(S_{i-1})$에 가까울수록, $D_i (x)$의 값이 감소할 겁니다.
그런데, $S_{i-1}$에서 $\max(S_{i-1})$을 제거하고, $A_i$를 추가한 집합 $S_i$에서 $\max(S_i) = B_i$임을 우리는 알고 있습니다. 그리고 이 상황의 전제 조건이 $B_i < \max(S_{i-1})$이죠.
다시 말해서 $S_{i-1}$에서 최댓값 $M_{first}$을 빼낸 뒤, 이 $M$보다는 작은 게 분명한 $A_i$ ($B_i = \max(S_i) < \max(S_{i-1})$이므로)를
넣은 집합 $S_i$에서 최댓값이 되는 $M_{second} = B_i$라는 말입니다.
따라서 $x \le B_i$를 만족하면서 $D_{i-1} (x)$를 최소로 만드는 $x = B_i$입니다.
위 경우에 이를 적용하면, $B_3 = A_3$이고, $B_3 < A_1$이므로 $B_2 \le B_3 (=A_3) < A_1$ 조건에 의해 $B_2 \neq A_1$인 상황에서
$B_2 \le A_3$을 만족하면서 $D_2 (x)$를 최소로 만드는 $x = A_3$입니다.
뭐 물론 이 두 조건을 만족하는 $x$의 구간에 $A_3$ 말고도 여러 값이 존재할 수 있고, 그 값을 선택할 수도 있겠습니다만
적어도 $x = A_3$가 두 조건을 만족한다는 건 자명하다는 얘기죠.

$S_i$에 속한 $B_i$가 아닌 다른 원소들 $others < B_i (=\max(S_i)) < \max(S_{i-1})$ 이므로,
$B_i$는 기울기가 0인 구간에 존재한다는 것을 알 수 있습니다.
그렇다면 $D_{i-1} (\max(S_{i-1})) = D_{i-1} (B_i)$ 이므로, 비용 역시 변함없이 최솟값을 유지할 수 있습니다.
정리하면 다음과 같습니다.
1. $\max(S_{i-1}) \le B_i$일 때, $B_{i-1} = \max(S_{i-1})$
2. $B_i < \max(S_{i-1})$일 때, $B_{i-1} = B_i$
다시 말해서 $B_{i-1}$는 둘 중 더 작은 값이 된다는 말이네요.
$B_{i-1} = \min(B_i, \max(S_{i-1}))$가 성립합니다.
정리하면
$B_{N} = \max(S_N)$,
$B_{i-1} = \min(B_i, \max(S_{i-1}))$ $, 1 < i \le N$
그러므로 $max(S_i)$를 저장해 뒀다가 $i=N$부터 역순으로 비교하면서 더 작은 값으로 설정해 주면 되겠습니다.
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
int N, A[...], B[...];
priority_queue<int> q;
int main()
{
... //get input to array A
for (int i = 0; i < N; i++)
{
q.push(A[i]);
B[i] = q.top(); //= max(S)
if (q.top() > A[i]) //A[i] < max(S)
{
q.push(A[i]);
q.pop();
}
}
for (int i = N - 1; i > 0; i--)
B[i - 1] = min(B[i], B[i-1]);
for (int i = 0; i < N; i++)
cout << B[i] << ' ';
return 0;
}
그런데 처음 예시 문제를 설명할 때, 문제에서는 수열 $B$의 조건이 $B_i \le B_{i+1}$ (단조 증가)가 아니라,
$B_i < B_{i+1}$ (강한 증가)라고 했습니다.
지금까지 이해하고 구현한 Slope Trick은, $B$가 단조 증가한다는 조건 하에 동작하기 때문에
수열을 단조 증가로 변환하여 푼 뒤에, 다시 강한 증가수열로 되돌려 줄 필요가 있습니다.
이를 위해서는 아이디어가 하나 필요합니다.
$B_i < B_{i+1}$이므로, $B_{i+1} - B_i > 0$, 즉 $B_{i+1} - B_i \ge 1$입니다.
$B$가 정수 수열이기 때문에 성립하네요. 일반화하면 수열의 값의 차이는 인덱스의 차이 이상일 거란 얘기입니다.
즉 $i < j$인 두 수 $i, j$에 대해 $B_i < B_j$가 성립하므로, $B_j - B_i \ge j - i$가 성립합니다.
식을 정리하면 $B_i - i \le B_j - j$입니다.
$C_i = B_i - i$를 정의해 봅시다. 이 새로운 수열 $C$에 대해서 $C_i \le C_{i+1}$이 성립합니다.
인덱스 $i$는 점화식을 푸는 동안 변하는 값이 아니니, $A_i - i$를 이용해 $C_i$를 구하고 여기에 다시 $i$를 더해서 $B_i$를 구할 수 있습니다.
이를 이용해 최소가 되는 값을 구하는 것이 백준 13323번이고,
수열 $B$를 구하는 것이 백준 13324번입니다.
근데 이거 응용해서 문제를 풀으라 한다면 저는 못할 듯;
'C++ > PS' 카테고리의 다른 글
| [BOJ/C++] shake! 2021 E ~ I번 (BOJ 24232, 24233, 24234, 24235, 24236) (0) | 2022.03.12 |
|---|---|
| [BOJ/C++] shake! 2021 A ~ D번 (BOJ 24228, 24229, 24230, 24231) (0) | 2022.01.21 |
| [BOJ/C++] 23744. 알고리즘 과외 (0) | 2022.01.05 |
| [BOJ/C++] 17476. 수열과 쿼리 28 (0) | 2021.12.27 |
| [BOJ/C++] 13263. 나무 자르기 (0) | 2021.12.22 |